Weaving with Curved Ribbons

Abstract

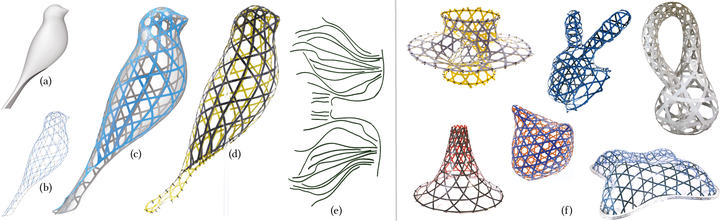
Basket weaving is a traditional craft for creating curved surfaces as an interwoven array of thin, flexible, and initially straight ribbons. The three-dimensional shape of a woven structure emerges through a complex interplay of the elastic bending behavior of the ribbons and the contact forces at their crossings. Curvature can be injected by carefully placing topological singularities in the otherwise regular weaving pattern. However, shape control through topology is highly non-trivial and inherently discrete, which severely limits the range of attainable woven geometries. Here, we demonstrate how to construct arbitrary smooth free-form surface geometries by weaving carefully optimized curved ribbons. We present an optimization-based approach to solving the inverse design problem for such woven structures. Our algorithm computes the ribbons’ planar geometry such that their interwoven assembly closely approximates a given target design surface in equilibrium. We systematically validate our approach through a series of physical prototypes to show a broad range of new woven geometries that is not achievable by existing methods. We anticipate our computational approach to significantly enhance the capabilities for the design of new woven structures. Facilitated by modern digital fabrication technology, we see potential applications in material science, bio- and mechanical engineering, art, design, and architecture.